کات ست؛ آموزش مدار الکتریکی 2 ؛ گرافهای شبکه و قضیه تلگان ؛ جلسه 5
- مهندسی برق, مدار 2
- نرگس دارابی
- 3 دقیقه
سلام و عرض ادب خدمت دوستان عزیزم؛ امیدوارم حال دلتون عالی باشه و همچنان با شور و اشتیاق ما را در ادامه مسیر همراهی کنید. امروز قصد داریم توی این جلسه به بررسی مفهوم کات ست بپردازیم. پس تا انتها با ما همراه باشید.
مقدمه: مفهوم کات ست در مدارهای الکترونیکی
در طراحی مدارهای الکترونیکی، کنترل و مدیریت جریان و ولتاژ اهمیت بالایی دارد. یکی از مفاهیمی که در این زمینه کاربردی است، «کات ست» (Cut Set) است. کات ست به مجموعهای از عناصر یا شاخههای مدار گفته میشود که اگر همگی آنها قطع شوند، مسیر جریان اصلی در مدار از بین میرود و مدار عملاً باز میشود. این مفهوم در تحلیل قابلیت اطمینان مدار، تشخیص نقاط بحرانی و طراحی سیستمهای حفاظتی اهمیت زیادی دارد. شناخت کات ستها به مهندسین کمک میکند تا نقاط ضعف مدار را شناسایی کرده و عملکرد پایدار و ایمن سیستم را تضمین کنند.
اما قبل از آشنایی با این مفهوم اجازه بدید یک موضوع پایه ای رو با هم مرور کنیم تا بعد به اصل ماجرا برسیم.
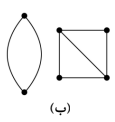
اگر میان هر دو گره دلخواه یک گراف، حداقل یک مسیر وجود داشته باشد (در روی شاخه های گراف و بدون در نظر گرفتن جهت شاخه ها) آن گراف را پیوسته گویند. به موجب قرارداد، گرافی که از یک گره تنها تشکیل می یابد، پیوسته است. گویند یک گراف پیوسته یک جزء جدا از هم دارد. در یک گراف ناپیوسته حداکثر تعداد زیر گرافها ی پیوسته را نیز جزءهای جدا از هم نامند. بنابراین یک گراف ناپیوسته باید حداقل دارای دو جزء جدا از هم باشد. گراف نشان داده شده در شکل (الف) پیوسته بوده در حالی که گراف شکل (ب) ناپیوسته است و دارای دو جزء جدا از هم می باشد.

برای توضیح مفهوم یک کات ست باید مشخص نمود که منظور از عبارت حذف یک شاخه چیست. وقتی می گوییم شاخه ای را حذف می کنیم ، منظور ما این است: قطعه خطی که دو گره را به هم وصل می کند حذف کرده و خود گره ها را نگه می داریم.
بریم ببینیم داخل جزوه این مبحث را چگونه بیان کرده ایم:
مفهوم کات ست
دسته ای از شاخه های یک گراف پیوسته را کات ست می نامند. چنانچه:
- حذف تمام شاخه های این دسته موجب شود که گراف باقی مانده دارای دو جز جدا از هم باشد.
- حذف تمام شاخه های این دسته به جز یکی از آنها یک گراف پیوسته باقی گذارد.
مطمان هستم مثل همیشه با یک مثال قضیه کامل براتون روشن خواهد شد.
مثال) در گراف نشان داده شده در شکل زیر:

الف) نشان دهید که هر یک از دسته شاخه های زیر یک کاست می باشد.
8,9 ,6 , 3, 2, 1 ، 7,9 ,6, 4, 2, 1 ، 5 , 2,4 ,1
ب) معادلات KCL هر کاست را بنویسید و هر یک از آنها را بر حسب ترکیب خطی از معادلات گره مناسب بیان کنید.
پ) ثابت کنید این کات ست ها نسبت به هم مستقل خطی هستند.
حل این مثال با من بعدی با شما:

به موجب KCL برای هر شبکه فشرده و در هر لحظه از زمان و برای هر یک از کات ستهای آن، مجموع جبری جریانهای تمام شاخه های کات ست، مساوی صفر است.
در یک گراف داده شده l و g را را حلقه گویند. اگر:
- l یک زیرگراف متصل به هم g باشد و
- به هر گره از l دقیقا دو شاخه از l متصل شده باشد.
خب این هم از این جلسه که براتون مفصل توی بخش محتوای ویدئویی توضیح دادم که براحتی می توانید از این لینک و نیز این آدرس آن را مشاهده کنید. بجز این مثال، مثالهای دیگه ای هم داخل جزوه هست که برای دیدن اونها باید به جزوهخ این فصل مراجعه کنید. برای تهیه جزوه این لینک در دسترس شما عزیزان قرار داده شده است.
همراهی شما عزیزان باعث دلگرمی ماست. ممنون این جلسه نیز ما را همراهی کردید.
موفق و پیروز باشید.










