آموزش مقاطع مخروطی با مهندس زوارقی؛ هذلولی؛ جلسه 1

عرض سلام و احترام خدمت شما دوستان عزیزم ایدوارم حال همگی خوب باشه. خب بسلامتی رسیدیم به آخرین مبحث در مقاطع مخروطی یعنی هذلولی.

اول بریم یک پیام محب آمیز از شما عزیزان رو با هم بخونیم ببینیم چی بوده:

یه روز که دنبال یادگیری هذلولی بودم، یهویی تو اینترنت به وبسایت و کانال یوتیوب مهندس زوارقی برخوردم. اولش فکر می‌کردم یه جورایی یه سایت عجیب و غریب پیدا کردم، ولی بعدش فهمیدم که آموزش‌های فوق‌العاده‌ای داره ارائه می‌ده.

تمرین‌ها و تست‌های این فصل واقعاً حسابی مفید بودن و به من کمک کردن تا اون موضوع سخت هذلولی رو بهتر بفهمم. الان با اعتماد به نفس میگم که این آموزش‌ها باعث شدن از پایه به یک سطح حرفه‌ای برسم.

واقعاً ممنونم از مهندس زوارقی؛ به تمام دوستانم که دنبال یادگیری مفاهیم پیچیده هستن، پیشنهاد می‌کنم حتماً یه سر به این منابع ارزشمند بزنید! امیدوارم ما هم برای ادای احترام به زحمات شما استاد بزرگوار از طریق قانونی و با رضایت شما از مطالب وبسایت و کانال تون استفاده کنیم.

بقول شما دوستان دهه های اخیر چشمام صورتی شد این پیام رو خوندم وکلی ذوق کردم که علاوه بر رضایت از آموزش، با وجدان و مسئولیت پذیر هم هستید. دم شما گرم واقعا. به پاس این حجم از درک و شعور بالای شما تصمیم گرفتم همچنان به آموزشهای کانالم ادامه بدم. چون رسالت من خیلی مهم و من بهش پایبندم.

بریم سراغ آخرین مبحث این فصل ریاضی. با من همراه باشید.

تعریف:

به مکان هندسی نقاطی از صفحه که قدرمطلق تفاضل فواصل آنها از دو نقطه ی ثابت صفحه مقدار ثابتی( کمتر از فاصله ی بین دو نقطه) باشد، هذلولی گویند. همانند بیضی به دو نقطه ی ثابت هذلولی کانون و فاصله ی دو کانون را با 2c نمایش می دهیم و همچنین مقدار ثابت هذلولی را با 2a نمایش می دهند. 

نمودار هذلولی به صورت زیر است که از دو شاخه مجزا تشکیل شده است و همانند بیضی دارای محور کانونی و محور ناکانونی بوده و نقاط برخورد محور کانونی با هذلولی را راسهای کانونی گوییم. در ضمن در هذلولی a>c است.

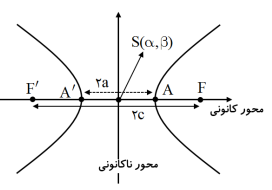
نمودار بالا، نمودار هذلولی افقی به مرکز (α,β)S است و فرم کلی آن به صورت 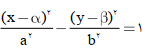است و معادله ی مجانبهای هذلولی افقی برابر است با

شکل کلی هذلولی قائم با مرکز (α,β)S، به صورت مقابل است.

فرم کلی این هذلولی برابر است با: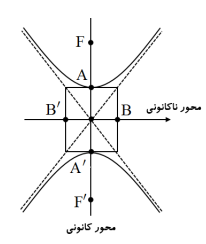

معادله ی مجانبهای هذلولی قائم برابر است: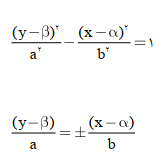

خواص کلی هذلولی:

1. اگر معادله ی هذلولی را به شکل استاندارد دربیاوریم، در صورتی که ضریب y² منفی باشد، افقی و در صورتی که ضریب x² منفی باشد، قائم است.
2. مرکز هذلولی مرکز تقارن آن و محورهای هذلولی، محورهای تقارن آن قائم است. 
3. در معادله ی استاندارد، همواره مخرج کسر مثبت، a² و مخزج کسر منفی، b² است.
4. در هذلولی افقی یا قائم شیب مجانبها قرینه ی یکدیگرند. (شیب مجانبهای هذلولی افقی برابر است و شیب مجانبهای قائم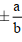است.) درضمن نقطه ی تلاقی مجانبهای هذلولی، مرکز است.
   
5. اگر در هذلولی a = b باشد، آنگاه به آن متساوی القطرین گویند. در این نوع، مجانبها بر هم عمودند و خروج از مرکز برابر e =√2 است. معادله ی متساوی القطرین با مرکز (0,0)O به صورت 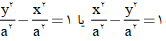است.
   
6. اگر خطوط مجانبهای هذلولی به صورت ax +by + c= 0, a’x +b’y +c = 0 باشند، آنگاه معادله ی هذلولی به صورت ( ax +by + c= 0) (a’x +b’y +c = 0) = λ می باشد. (λ عدد ثابت است.)
7. اگر معادله ی هذلولی f = 0 باشد، مختصات مرکز از رابطه ها f’_x = 0 ,f’_y = 0  بدست می آید.

اینم مثال برای حسن ختام جلسه: 

هذلولی زیر را رسم کنید:

9x²  – 4y² – 36x – 24y – 36 = 0

تا اینجا این جلسه رو داشته باشید و جمع بندی کنیم.

شما میتونید برای دیدن توضیحات تکمیلی همراه حل تمرین و مثال به کانال یوتیوب ما توی این لینک مراجعه کنید. جزوه این جلسه هم که از فروشگاه وبسایت مون توی این آدرس، براحتی قابل تهیه است.

تا جلسه ی بعد خدانگهدار

موفق باشید🍀