آموزش و مرور توزیع احتمال توام؛ آمار و احتمال مهندسی؛ جلسه 9

سلم و عرض ادب خدمت دوستان عزیزم؛ امیدوارم حال دلتون عالی باشه. امروز قصد داریم به بررسی توزیع احتمال توام در مباحث آمار مهندسی بپردازیم. پس تا انتها همراه ماباشید.

مقدمه‌ای بر توزیع احتمال توأم (Joint Probability Distribution)

در دنیای آمار و احتمال، بسیاری از پدیده‌ها را نمی‌توان تنها با یک متغیر تصادفی توصیف کرد. گاهی لازم است رفتار هم‌زمان دو یا چند متغیر را بررسی کنیم؛ اینجاست که مفهوم توزیع احتمال توأم وارد می‌شود. این توزیع، به ما نشان می‌دهد که احتمال وقوع هم‌زمان دو رویداد یا دو مقدار خاص از دو متغیر تصادفی چقدر است. درک درست این مفهوم، پایه‌ای ضروری برای تحلیل‌های آماری پیچیده‌تر مانند کوواریانس، همبستگی، و مدل‌سازی‌های چندمتغیره است.

توزیع احتمال توأم

تعریف: اگر X,Y دو متغیر تصادفی باشند (z(X,Y را کهیک متغیر تصادفی توام یا دو بعدی نامند.  اگر X,Y هر دو گسسته باشند، z را گسسته و اگر X,Y پیوسته باشند، را پیوسته و اگر یکی از X,Y پیوسته و دیگری گسسته باشد، z را آمیخته گویند. ثلاً اگر از کیسه ای که محتوی 5 مهره قرمز، 3 مهره آبی و 4 مهره سبز است، 4 مهر انتخاب کنیم و منظور از این آزمایش، تعیین تعداد مهره های قرمز و آبی و سبز در این نمونه انتخاب شده به صورت همزمان باشد، در این صورت یک فضای نمونه های سه بعدی داریم. فعلاً از فضای نمونه های دوبعدی بحث میکنیم. در فضای نمونه ای دوبعدی به طور همزمان دو هدف را دنبال میکنیم. اگر هدف اول X و هدف دوم Y باشد، به طور همزمان دو متغیر تصادفی خواهیم داشت که زوجهای مرتبی مانند  (x, y) را اختیار خواهند کرد. در حالت گسسته می توان نوشت:

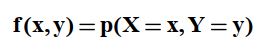
به عبارت دیگر (f(X,Y نشان دهنده احتمال آن  است که در پایان آزمایش تعداد x  موفقیت از متغیر تصادفی x  و تعداد y موفقیت از متغیر تصادفی y داشته باشیم.

مثلاً از کیسه ای که محتوی 5 توپ قرمز و 4 توب آبی، سه توپ را به تصادف و بدون جایگذاری انتخاب می کنیم. متغیر x  نشان دهنده تعداد توپ قرمز و متغیر تصادفی Y نشاندهنده تعداد توپ آبی در این نمونه باشد، (1 2) f نشان دهنده مقدار احتمال پیشامد ای است که در آن نمونه سه تایی، دو توپ قرمز و یک توپ آبی است.

یعنی:

در حالتی که X,Y یا هر دو گسسته باشند، F_x,y(x,y) توزیع احتمال توام و در حالتی که X,Y هر دو پیوسته باشند، F_x,y(x,y)  را تابع چگالی احتمال توام می ‌نامیم.

 الف) خصوصیات توزیع احتمال توام (گسسته)

تابع F_x,y(x,y) را توزیع احتمال توام دو متغیر X,Y گسسته مینامیم اگر:

اگر x , y هر دو گسسته باشند،  F_x,y(x,y) را به صورت جدول هم می توان نوشت.

ب) خصوصیات تابع چگالی احتمال توام (پیوسته)

تابع F_x,y(x,y) را تابع چگالی دو متغیر تصادفی پیوسته X,Y  می ‌نامیم اگر: مثال) از جعبه ای که محتوی 3 خودکار آبی، 2 خودکار قرمز و 3 خودکار سبز است، دو خودکار را به تصادف و بدون جایگذاری بیرون می آوریم. در صورتی که متغیر تصادفی X نشان دهنده تعداد خودکار آبی و Y نشاندهنده تعداد خودکار قرمز باشد.
الف) توزیع احتمال توام را به دو صورت جدولی و فرمولی بنویسید.

ب) احتمال پیشامد  را حساب کنید.

برای دیدن جواب و حل این مثال حتما به لینک آموزش ویدئویی در کانال یوتیوب و وبسایت ما مراجعه کنید. بخاطر داشته باشید حتما جزوه این جلسه را هم تهیه کنید که براحتی از این لینک قابل دسترسی است.

مثل همیشه سپاسگزارم که این جلسه نیز ما را هراهی کردید. 

موفق باشید.