آموزش فضاهای برداری جبر خطی ؛ مستقل خطی یا وابسته خطی ؛ جلسه 15

درود و عرض ادب خدمت دوستان عزیزم؛ مطمان هستم روزهای آغازین فصل پاییز و درس و دانشگاه، انگیزه و تلاش شما را چندین برابر کرده است. با این امید بریم سراغ مطلب امروز که به بررسی استقلال خطی خواهیم پرداخت.  تا انتهای این آموزش نیز همراه ما باشید.

استقلال خطی

یکی از مفاهیم پایه‌ای در جبر خطی، استقلال خطی بردارها است. بردارها زمانی مستقل خطی هستند که هیچ برداری از آن‌ها را نتوان با ترکیب خطی دیگر بردارها به دست آورد. به عبارت دیگر، هیچ برداری در مجموعه، وابسته به دیگر بردارها نیست. این ویژگی اهمیت زیادی دارد، چرا که به ما کمک می‌کند تا مجموعه‌ای از بردارهای پایه یا فضای برداری مستقل بسازیم و ابعاد فضاها، حل دستگاه‌های معادلات خطی و بسیاری مفاهیم دیگر در ریاضیات و علوم مهندسی را بهتر درک کنیم.

گردآورده(مولد) { x₁,x₂,…,x_n} از بردارهای یک فضای برداری را مستقل خطی گوییم اگر:  α₁x_{1 +} α₂x₂ + … α_nx_n = 0    ایجاب کند . به عبارت دیگر، اگر تنها ترکیب خطی از x₁,x₂,…,x_n که مساوی صفر است، ترکیب زیر باشد:

برای مثال در _R² بردارهای مستقل خطی اند. زیرا اگر فرض کنیم: 

به عنوان مثالی دیگر، در P₂ مجموعه چند جمله ای های با ضرایب حقیقی و با درجه نابیشتر از ،2 بردارهای مستقل خطی اند. زیرا:

پس یک مجموعه مستقل خطی از بردارهاست.

برای همین قضیه براتون چندین مثال داخل جزوه قرار دادم که سعی کنید اول خودتان حل کنید بعد به آموزش ویدئویی این جلسه در این لینک مراجعه کنید که با جزئیات کامل براتون شرح دادم. از جزوه هم غافل نشید که تمام مطالب محتوای وبسایت را پوشش میدهد. برای دریافت جزوه به این آدرس مراجعه کنید.

یک مثال را براتون حل می کنم بقیه با شما.

مثال) در فضای ماتریسهای M₂₂ ، 2 × 2 کدام یک یا از مجموعه های زیر مستقل خطی اند؟

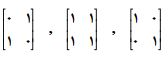
حل:

کل محتوای آموزش ویدئویی این فصل هم از این لینک قابل تهیه هست.

خب این هم از جلسه امروزز. امیدوارم براتون کاربردی بوده باشد. اگز نکته ای در جهت بهبود آموزش به نظرتان رسید، مشتاقانه شنیدن نظرات شما عزیزان هستیم.

موفق باشید.