قضیه گرین به زبان ساده با مهندس زوارقی؛ ریاضی عمومی 2

سلام و عرض ادب خدمت دوستان عزیزم امیدوارم حال دلتون عالی باشه. در ادامه مباحث مربوط به انتگرال خط، امروز قصد داریم به یک مبحث مهم دیگه بپردازیم با عنوان قضیه گرین.

در دنیای ریاضیات، به‌ویژه در مباحث مربوط به حساب دیفرانسیل و انتگرال برداری، قضیه گرین یکی از ابزارهای قدرتمند برای تحلیل میدان‌های برداری در صفحه دوبعدی به شمار می‌آید. این قضیه، پلی زیبا میان انتگرال‌های خطی و انتگرال‌های سطحی برقرار می‌کند و به ما اجازه می‌دهد تا اطلاعات کلی درباره‌ی یک ناحیه را تنها با بررسی مرز آن به دست آوریم.

به زبان ساده، قضیه گرین بیان می‌کند که چرخش یک میدان برداری درون یک ناحیه بسته، با جریان آن میدان روی مرز آن ناحیه مرتبط است. این ارتباط مفهومی، نه‌تنها در ریاضیات نظری اهمیت دارد، بلکه در فیزیک (برای مثال در تحلیل میدان‌های مغناطیسی و الکتریکی) و مهندسی (مانند مکانیک سیالات) نیز کاربردهای فراوانی دارد.

در این مطلب، به بررسی دقیق‌تر قضیه گرین، مفاهیم مرتبط با آن، شرایط لازم برای استفاده، و مثال‌هایی کاربردی خواهیم پرداخت.

تعریف خم های بسته ساده

خم های بسته ساده خم هایی هستند که خود را قطع نمی کنند. مثل دایره، بیضی، مربع یا مستطیل. اما شکل هایی مانند نماتید بی نهایت چنین نیستند.

قضیه گرین: فرض کنید C یک منحنی بسته ساده و جهت دار باشد که در جهت مثلثاتی طی شده و D ناحیه ای مسطح در صفحه xoy باشد که توسط منحنی c محصور شده است. اگر P,Q توابع با مشتقات جزئی پیوسته در D باشد آنگاه داریم: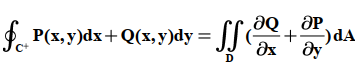

جهت صحیح مثبت در قضیه گرین و تساوی فوق به این صورت است که وقتی بر روی منحنی حرکت می کنیم ناحیه در سمت چپ ما باشد.

یک مثال در این مورد با هم حل کنیم تا قضیه روشن تر بشه.

مثال) اگر و C محیط ناحیه باشد که در جهت مثلثاتی طی می شود، مقدار Fdr∫ کدام است؟

حل)

چون مسیر بسته است، پس از قضیه گرین استفاده می کنیم:

اگر بخواهیم کل محتوای چند جلسه مرتبط با این عنوان از جزوه را اینجا براتون بیارم، این پست خیلی طولانی میشه و ما قصد داریم با تولید محتوای کوتاه، مطالب مهم را برای شما معرفی کنیم تا برای مطالعه کامل اونها اولا به جزوه از این لینک و محتوای کامل آموزشی ویدئویی از این لینک و این لینک مراجعه کنید. 

مثل همیشه منتظر شنیدن نظرات سازنده شما هستیم تا روند کارمون رو ارتقا بدیم.

موفق باشید.