آموزش فضای برداری جبر خطی با مهندس زوارقی؛ جلسه 1

سلام و عرض ادب خدمت دوستان عزیزم امیدوارم حالتون خوب باشه و کماکان برای یادگیری مطالب جدید پیگیر باشید. رسیدیم به فصل سوم از مبحث جبر خطی و فضاهای برداری.

فضای برداری: مجموعه ای مانند V است مرکب از اشیائی به نام بردار، با دو عمل تعریف شده بر روی آن: جمع، و ضرب اسکالر

جمع بردارها به این معنی است که با مفروض بودن دو بردار x, y در V قاعده ای وجود دارد که برداری مانند x + y را که آن نیز در V است، معین می کند و این بردار را حاصل جمع x, y می نامند. منظورمان از ضرب اسکالر، قاعده ای است که به هر بردار x در V و هر اسکالر حقیقی ، یک بردار x در V نسبت می دهد. این بردار را مضرب اسکالر بردار x با ضریب اسکالر می نامند.

گیریم V مجموعه ای باشد که برای آن جمع و ضرب اسکالر بردارها تعریف شده اند، و گیریم x, y, z متعلق به V و α,β اعدادی حقیقی باشند. اصول فضای برداری عبارت اند از :

خاصیت جابجایی
خاصیت شرکت پذیری
وجود عنصر صفر
وجود عنصر قرینه

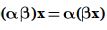
مجموعه ای مانند V را که اعمال تعریف شده بر آن در فهرست شرایط فوق صدق کنند، فضای برداری حقیقی یا فضای برداری روی اعداد حقیقی می خوانند. بردار صفر را که وجودش در V به عنوان اصل پذیرفته شده است بردار صفر و بردار x- را منفی یا قرینه بردار x می نامند.

فضای برداری مختلط: به طریق مشابه تعریف می شود. فقط این را به عنوان اصل می پذیریم که مضرب اسکالر بردار x با ضریب اسکالر α برای هر x در V و هر عدد مختلط ، تعریف شده است.

خب بریم این جلسه رو با یک مثال به پایان ببریم که برای دیدن جواب این تمرین، حتما به ویدئوی آموزشی این مبحث از توی این لینک می تونید دسترسی داشته باشید.

مثال) فضای برداری را در سه تابع زیر بررسی کنید:

دوستان عزیزم، می دونید که جزوه هر فصل کامل بصورت تایپ شده قابل تهیه است که برای تهیه جزوه این فصل هم می تونید به این آدرس از فروشگاه بسایت مون مراجعه کنید.

باز هم ممنونم که همراه همیشگی ما هستید و ما رو با دادن نظرات سازنده در ادامه این مسیر حمایت می کنید.

تا جلسات بعدی

موفق و کامروا باشید.