صفر تا صد محاسبات عددی؛ جلسه 5؛ حالت نمایی

سلام و عرض ادب خدمت دوستان عزیز؛ امیدوارم حال دلتون عالی باشه. امروز قصد داریم در ادامه مباحث محاسبات عددی به بررسی حالت نمایی بپردازیم. بدون معطلی بریم سراغ آموزش امروز. با ما همراه باشید.

حالت نمایی

در بسیاری از مسائل ریاضی و مهندسی، معادلات دیفرانسیل با رفتارهایی ظاهر می‌شوند که رشد یا واپاشی آن‌ها به صورت نمایی است. تحلیل و تقریب عددی چنین سامانه‌هایی اهمیت ویژه‌ای دارد، زیرا کوچک‌ترین خطاهای محاسباتی می‌توانند در طول زمان به صورت نمایی تقویت یا تضعیف شوند. از این رو، معرفی و بررسی حالت نمایی در محاسبات عددی، ابزاری بنیادی برای درک پایداری روش‌های عددی، بررسی رفتار بلندمدت جواب‌ها، و تضمین دقت در الگوریتم‌های محاسباتی به شمار می‌رود.

با این مقدمه کوتاه بریم سراغ مباحث داخل جزوه.

در خیلی از مسائل، تقریب به وسیله چند جملهای مناسب نیست زیرا وقتی (x_i , y_i) ها را در یک دستگاه مختصات رسم می کنیم، ممکن است مجموعه نقاط رسم شده شبیه یک منحنی نمایی هذلولی و یا یک منحنی مثلثاتی باشد.

هرگاه x_iها و lny_i ها را در یک دستگاه مختصات رسم کنیم و رابطه ای خطی بین (x_i , lny_i ) ها ظاهر شود، در چنین حالتی معقول است که تقریبی به صورت زیر در نظر بگیریم. 

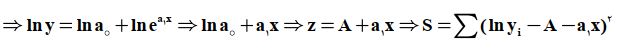
بریم یک مثال حل کنیم تا این قضیه هم برامون جا بیفته:

مثال) داده های جدول زیر را در نظر بگیرید. اگر x_iها با lny_i ها رسم شوند، معلوم میشود که داده ها رابطه ای خطی دارند. لذا تقریب حداقل مربعات برای برازش داده های فوق به صورت نمایی است. این تابع نمایی را تعیین کنید.

بریم حل کنیم بعد جدول اش را ایجاد کنم براتون:

اینم جدول:

خب این هم از توضیحات آموزشی این جلسه. برای دیدن توضیحات کامل حتما به آموزش ویدئویی این جلسه در این لینک مراجعه کنید. حتما در کنار آموزش های وبلاگ از مطالعه جزوه هم غافل نشید که برای دریافت جزوه براحتی می توانید به این آدرس در فروشگاه مراجعه کنید.

از اینکه این جلسه هم ما را همراهی کردید، سپاسگزاریم. لطفا با ارسال نظرات سازنده تان، از ما حمایت کنید.

موفق باشید.