حل معادلات عددی به روش نیوتن در محاسبات عددی؛ جلسه 6

سلام و عرض ادب خدمت دوستان عزیزم؛ امیدوارم حال دلتون عالی عالی باشد و همچنان همراه ما باشید. امروز و در این جلسه قصد داریم به یک روش دیگر در حل معادلات عدی بپردازیم با عنوان روش نیوتن. با ما همراه باشید با یک مقدمه کوتاه.

روش نیوتن

یا Newton-Raphson یکی از پرکاربردترین روش‌های محاسبات عددی برای یافتن ریشه‌های یک معادله غیرخطی است. ایده اصلی این روش بر پایه تقریب تابع با یک خط مماس در نقطه‌ای دلخواه و یافتن محل برخورد این خط با محور افقی بنا شده است. با تکرار این فرایند می‌توان به سرعت به جواب دقیق نزدیک شد، به شرطی که حدس اولیه مناسب باشد و تابع در اطراف ریشه رفتار مناسبی داشته باشد. روش نیوتن به دلیل سرعت همگرایی بالا، به‌ویژه در مسائل علمی و مهندسی، بسیار محبوب است.

همانگونه که در شکل زیر دیده می شود، α ریشه مورد نظر است.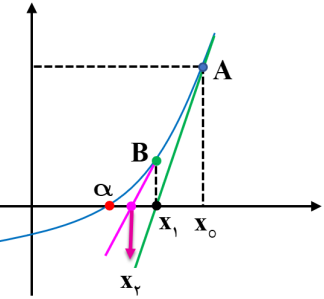

هر گاه X_O تقریبی از ریشه باشد، از نقطه A(X_O , f(X_O )) واقع بر منحنی Y= f(x) مماس بر منحنی را رسم کنیم. محل تلاقی این مماس، با محور طولها را X₁ می نامیم. سپس ازنقطه B(X₁, f(X₁ )) واقع بر منحنی، مماس را رسم می کنیم و محل تلاقی این مماس جدید را با محور طولها X_{2 می نامیم. این عمل را آنقدر تکرار می کنیم تا Xn به اندازه کافی به ریشه یعنی α نزدیکتر شوند.}

ابتدا با داشتن X_o برای تعیین X_{1 ،} باید معادله خط مماس بر منحنی Y= f(x) را بنویسیم (در نقطه (X_O , f(X_O )) ) و محل تلاقی آن را با محور xها تعیین کنیم. پس داریم:     

حال محل تلاقی این خط را با محور طولها یعنی (X_{1 , 0} ) را بدست می آوریم:

که اگر f’ (X_o) ≠ 0 باشد، داریم:

 و  در حالت کلی داریم:

رابطه(*) را روش تکرار نیوتن گویند.

یک مثال رو براتون اینجا میارم تا بیشتر متوجه موضوع شوید:

مثال1) ریشه معادله f(x) = x – cosx = 0 را که در فاصله [ 1 ,0 ] قرار دارد، به روش نیوتن با چهار رقم اعشار بدست آورید. به طوریکه  که X_n  تقریب ریشه مورد نظر در تکرار n ام است و قرار دهید X_{o = 0/5}

حل مثال را هم ببینیم:

چونلذا X₃  تقریب مورد نظر هست. α ≈ 0/7391

بریم دو تا نکته بگیم و این جلسه رو به پایان برسونیم:

نکته1) در این روش اگر در این مثال تقریبها را ادامه دهیم، ریشه های همان ریشه خواهد بود:

نکته2) تعداد تکرار در این روش کمتر از روشهای قبلی است.

خب این جلسه هم در این حد کافی هست و طولانی تر نکنیم. 

برای دیدن مثالهای بیشتر به ادامه جلسات در جزوه از این لینک اقدام کنید. فراموش نکنید همزمان با مطالعه جزوه به محتوای ویدئویی هم در این آدرس و این آدرس از کانال یوتیوب ما مراجعه کنید و کلیه مطالب را با جزئیات و دقیق یادداشت برداری کنید.

باز هم ممنون که تا انتها با ما همراه بودید. برای ادامه این جلسات هم منتظر همراهی شما عزیزان هستیم.

موفق و پرتوان بمانید.