جبر خطی؛ ماتریس و حل دستگاه معادلات خطی با مهندس زوارقی؛ جلسه 1

سلام و عرض ادب خدمت دوستان عزیزم. امیدوارم حال دلتون عالی باشه. 

رسیدیم به فصل اول از جبرخطی. بریم این فصل رو هم با انرژی مضاعف شروع کنیم. با من همراه باشید.

اعمال جبری روی ماتریس ها:

1- جمع و تفریق ماتریس ها: جمع و تفریق دو ماتریس فقط در صورتی تعریف پذیر است که دو ماتریس هم اندازه باشند در این صورت با یک مثال توضیح میدهم. 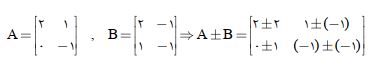2- ضرب اسکالر در ماتریس: اگر عدد اسکالری در ماتریسی ضرب شود، باید آن عدد به تک تک درایه های ماتریس ضرب شود.

مثال) اگر ماتریس A به صورت زیر باشد، آنگاه 2A را بدست آورید.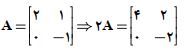 3- ضرب یک ماتریس: ضرب دو ماتریس در صورتی امکانپذیر است که تعداد ستونهای ماتریس اول با تعداد سطرهای ماتریس دوم برابر باشد با کمک ویدیوها به مثال زیر توجه کنید.

در ضمن ضرب خاصیت جابجایی ندارد.

مثال) اگر A,B دو ماتریس به قرار زیر باشد، AB,BA را بدست آورید.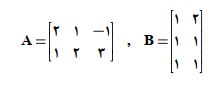حل این تمرین رو هم با هم ببینیم:

ترانهاده یک ماتریس: برای به دست آوردن ترانهاده یک ماتریس، کافیست جای سطر و ستون آن ماتریس را عوض کنیم.

مثال)

اگر A یک ماتریس باشد، شرط لازم برای به دست آوردن ، Aⁿ  این است که ماتریس مربعی باشد. 

ماتریس قطری: به ماتریس مربعی گویند که به غیر از درایه های قطر اصلی که غیرصفر هستند، بقیه درایه ها صفر هستند. مثال:

ماتریسهای بالا مثلثی و پایین مثلثی:

ماتریس A را بالا مثلثی میگوییم، هرگاه تمام درایه های زیر قطر اصلی آن صفر باشند. یعنی ماتریسی که در آن به ازای هر i >j داشته باشیم a_{ij = 0. به همین ترتیب ماتریس A را پایین مثلثی میگوییم، هرگاه تمام درایه های روی قطر اصلی آن صفر باشند. یعنی ماتریسی که در آن به ازای هر i < j داشته باشیم aij = 0.}

خب این هم از جلسه اول این فصل.

یادتون هست که همیشه روی این نکته تاکید دارم که یادگیری موثر این سبک آموزش نیازمند استفاده همزمان از تمام منابع موجود در این زمینه هست. پس برای تهیه جزوه این فصل شما می تونید به این لینک از فروشگاه وبسایت ما مراجعه کنید. ویدئوی این فصل هم از این لینک قابل تهیه و مشاهده هست.

لطفا با نوشتن نظرات تون در زیر همین پست ما را از روند فعالیت آموزشی مان مطلع بفرمایید.

تا جلسه بعدی

موفق باشید