آموزش مقاطع مخروطی؛ ریاضی کنکور؛ سهمی با مهندس زوارقی؛ جلسه 1

سلام و عرض ادب خدمت شما دوستان نازنینم. امیدوارم حالتون خوب باشه و اگر آزمونی داشتید با موفقیت سپری کرده باشید. رسیدیم به مبحث سهمی در مقاطع مخروطی. توی پست قبلی با مقاطع مخروطی آشنا شدیم.

همین اول جلسه میخوام یک تشکری داشته باشم از شما دوستان عزیزی که ما را در مسیر آموزشی همراهی میکنید و تشکر کنم از شما دوستانی که پیامهای محبت آمیزی جهت ادامه این مسیر برامون ارسال میکنید. قبل از شروع جلسه بریم یکی از پیامهای دوستان تون رو با هم بخونیم:

به عنوان یک دانش‌آموز کنکوری، تجربه من با آموزش‌های مهندس زوارقی در مورد مبحث سهمی‌های ریاضی فوق‌العاده مفید بود. ایشان با روش تدریس ساده و روان، مفاهیم پیچیده را به شکلی کاملاً قابل فهم توضیح می‌دهند. نکته‌ای که آموزش‌های ایشان را متمایز می‌کند، ارائه نکات تستی کاربردی و تحلیل دقیق سوالات کنکوری است که به درک عمیق‌تر و افزایش سرعت حل تست‌ها کمک زیادی می‌کند. علاوه بر این، در ویدیوهای یوتیوب و وبسایت، مثال‌های متنوعی بررسی می‌شود که باعث تثبیت بهتر مطالب در ذهن می‌شود. پیشنهاد می‌کنم اگر در این مبحث مشکل دارید، حتماً از آموزش‌های مهندس زوارقی استفاده کنید.

قدردان این محبت شما هستم و خدا رو شاکرم توی مسیر یادگیری شما عزیزان توانستم قدمی کوچک بردارم. با اجازه همگی بریم سراغ مطلب امروز. با من همراه باشید تا بریم یک مبحث مهم دیگه از مقاطع مخروطی یعنی سهمی.

تعریف: به مکان هندسی نقاطی از صفحه که از یک نقطه ی ثابت و یک خط ثابت در صفحه به یک فاصله باشد، را سهمی گوییم.

توضیحات مهم:

به نقطه ی ثابت سهمی، کانون و به خط ثابت آن، خط هادی گوییم. (F کانون است.)
به خطی کهاز کانون به خط هادی سهمی عمود می شود، محور سهمی می گوییم.
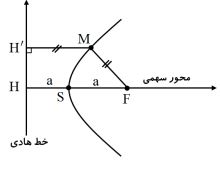
اندازه جبری کانون تا خط هادی برابر با 2a است.
به نقطه تلاقی محور سهمی، با سهمی را راس سهمی گویند (S راس سهمی است.) و اگر M نقطه ای روی سهمی باشد، آنگاه ‘MF=MH است.
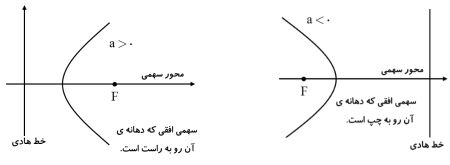
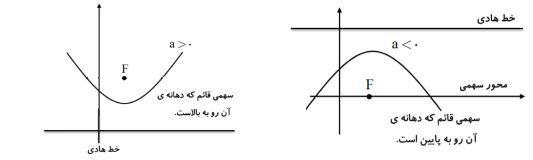
اگر محور سهمی، موازی محور xها باشد، به آن سهمی افقی و با توجه به علامت a دهانه ی سهمی به سمت راست یا چپ باز می شود و اگر محور سهمی، موازی محور y ها باشد، به آن سهمی قائم و با توجه به علامت a دهانه ی سهمی به سمت بالا یا پایین باز می شود.

معادلات سهمی:

در سهمی افقی با راس (α,β)S داریم: و مختصات کانون برابر است با: (a+α,β)F و معادله ی خط هادی x=α-a و معادله محور برابر است با y = β

در سهمی قائم با راس (α,β)S داریم و مختصات کانون برابر است با:(α,a+β)F و معادله ی خط هادی Y = -a+β و معادله ی محور برابر است با x = α

با توجه به معادلات سهمی، اگر توان 2 داشته باشد، افقی و اگر توان 2 داشته باشد، قائم است.

خب اینم از جلسه امروزمون که براتون توی کانال یوتیوب مون با مثال و حل تمرین، سعی کردم کاملا متوجه بشید. برای دیدن آمورش ویدئویی جلسه مقاطع مخروطی و سهمی به کانال یوتیوب ما مراجعه کنید. میدونید که جزوه تمام آموزشهایی که براتون میذارم هم داخل فروشگاه وبسایت مون موجود هست که برای تهیه جزوه این جلسه هم میتوانید به این آدرس مراجعه کنید.

مثال) هر یک از سهمی های زیر را رسم کنید: