آموزش ماتریس هسین(هسیان) با مهندس زوارقی؛ ریاضی عمومی 2

سلام و عرض ادب خدمت دوستان عزیزم ؛ امروز و توی این جلسه قصد داریم به یک مبحث جذاب در ریاضی عمومی 2 بپردازیم: ماتریس هسین. اگر آماده اید بریم سراغ این موضوع.

ماتریس هسین (Hessian Matrix) یک ابزار ریاضی مهم در حسابان است که برای تجزیه و تحلیل ویژگی‌های یک تابع چندمتغیره استفاده می‌شود. این ماتریس از مشتقات دوم یک تابع تشکیل شده و به‌ویژه در بهینه‌سازی، تحلیل رفتار توابع و شبیه‌سازی‌های عددی کاربرد فراوانی دارد. در بسیاری از مسائل پیچیده مانند پیدا کردن نقاط مینیمم و ماکزیمم تابع یا بررسی نوع منحنی‌ها، ماتریس هسین نقش کلیدی ایفا می‌کند. 

بررسی نقاط بحرانی و اکسترمم نسبی در توابع n متغیره:

تعریف: نقطه P را نقطه بحرانی گوییم، هرگاه(p)f∇ و اگر (p)f∇ موجود نباشد، p را نقطه تکین (ایزوله منفرد) می نامیم.

توجه) نقطهای که بحرانی یا ایزوله نباشد، را نقطه عادی یا ساده می نامیم.

ماتریس هسین: ماتریس هسیان به صورت زیر تعریف می شود:

برای شناسایی نوع نقاط بحرانی از آزمون مشتق دوم استفاده می کنیم.

آزمون مشتق دوم: فرض کنید P یک نقطه بحرانی برای F: R” → R و این تابع دارای مشتقات مرتبه دوم پیوسته باشد و داریم:

الف) اگر (H(P مثبت معین باشد، P نقطه می نیمم f است.

ب) اگر (H(P منفی معین باشد، P نقطه ماکزیمم f است.

ج) اگر (H(P نامعین باشد، P نقطه زینی f است.

د) اگر det(H(P)) 0 باشد، این آزمون بی نتیجه است.

مثال) نوع نقاط بحرانی تابع زیر را مشخص کنید. (اولی را من براتون حل میکنم. دو.می با شما)

f(x,y,z) = x²y + x²z + z² -2x

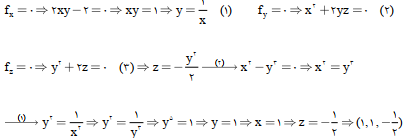
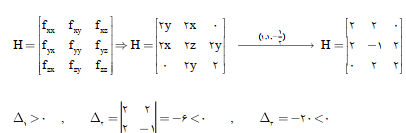
بنابراین H نامعین و P زینی یا زین اسبی است.

مثال دوم با شما:

خب این هم یک جلسه دیگر از مباحث کاربرد مشتق. برای دیدن توضیحات کامل به این لینک در کانال یوتیوب ما میتونید مراجعه کنید و یا از این لینک از داخل وبسایت مون این دوره آموزشی را تهیه کنید. حتما خاطراتون هست که همیشه تاکید دارم برای استفاده همزمان از جزوه و محتوای آموزشی. برای تهیه جزوه هم میتونید به این آدرس مراجعه کنید.

ممنون که مثل همیشه ما را تا پایان همراهی کردید.

تا جلسه بعدی 

موفق باشید🍀