آموزش انتگرال؛ ریاضی 1؛ جلسه 1 با مهندس زوارقی

سلام دوستان خوبم امیدوارم حال دلتون عالی باشه.

در ادامه مباحث ریاضی عمومی یک رسیدیم به فصل انتگرال. پس برای شروع لازم هست که فصلهای قبلی یعنی مشتق و کاربرد مشتق را یاد گرفته باشید تا راحت تر بتونیم این جلسه رو پیش ببریم. پس همره من باشید در این سری از آموزشهای جدید.

همین اول گفتنی ها رو بگیم و بریم سراغ درس امروز😉

فقط محض یادآوری و اونم اینکه میدونید که محتوای ویدئوهای کانال یوتیوب من، بسیار جامع و کامل و دربرگیرنده تعاریف به همراه حل تمرین ها و تست های داخل جزوات و پستهای وبلاگمون هست.

پس برای دیدن ویدئوی این آموزش کانال یوتیوب ما را حتما مشاهده کنید و جزوه مربوط به این فصل رو هم از این آدرس تهیه بفرمایید تا با نظم و انسجام آموزش های این درس شیرین را پیش ببرید.

انتگرال‌گیری یکی از مفاهیم بنیادی در حساب دیفرانسیل است و به همراه مشتق‌گیری، هسته اصلی این شاخه از ریاضیات را تشکیل می‌دهد. در حالی که مشتق‌گیری تغییرات یک تابع را توصیف می‌کند، انتگرال‌گیری به محاسبه مساحت زیر نمودار یک تابع، حجم، یا جمع کل مقادیر یک متغیر در بازه‌ای مشخص می‌پردازد.

این دو عمل، که رابطه‌ای عمیق و متقابل با یکدیگر دارند، ابزارهای اساسی برای تحلیل پدیده‌های طبیعی و حل مسائل مهندسی، فیزیک و علوم کاربردی هستند.

انتگرال‌گیری را می‌توان به دو دسته کلی تقسیم کرد: معین که به بازه‌ای خاص محدود است و نامعین که به شکل کلی‌تر عمل می‌کند و ثابت انتگرال را نیز در بر می‌گیرد. (نامعین رو توی این فصل جدی بگیرید چون با تسلط بر این بخش میتونید به تمام سوالات معین هم جواب بدید.)

تعریف تابع اولیه: F(x) را تابع اولیه ی f(x) گوییم هرگاه. بدیهی است اگر F(x) یکی از توابع اولیه ی f(x) باشد، F(x) + c نیز تابع اولیه ی f(x) است.

انتگرال نامعین: گوییم انتگرال f(x)dx برابر F(x) است، هرگاه d(F(x)=f(x)dx باشد.

حال آنکه مقدار انتگرال معین یک عدد ثابت است.

خب بریم سراغ قوانین و قواعد انتگرال:

توی این جلسه 5 مورد از این قواعد رو با هم بررسی میکنیم:

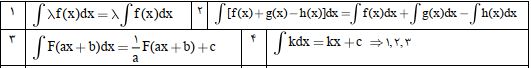
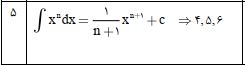
خیلی خوشحالم که این جلسه هم تا انتها همراه من بودید. یادتون نره زیر این پست، کامنت بذارید و بهم کمک کنید در بهبود ارائه مطالب باکیفیت و مفید برای شما عزیزانم.😊

موفق باشید