شرایط در مشتقات جزئی در حل معادلات دیفرانسیل؛ ریاضیات مهندسی؛ جلسه 3

سلام و عرض ادب خدمت دوستان عزیزم، امیدوارم حال دلتون عالی باشد. امروز در ادامه مباحث مشتقات جزئی قصد داریم به شرایط حاکم در حل معادلات دیفرانسیل درمشتقات جزئی بپردازیم. پس تا انتها همراه ما باشید.

معادلات دیفرانسیل جزئی (PDE) ابزار قدرتمندی برای توصیف پدیده‌های مختلف علمی، از جریان سیالات و انتقال گرما تا انتشار امواج، هستند. یکی از مراحل مهم در مطالعه این معادلات، مشخص کردن شرایطی است که تحت آن می‌توان پاسخ‌های یکتا، پایدار و معنادار به دست آورد. این شرایط، که به‌عنوان شرایط مشتقات جزئی شناخته می‌شوند، نقشی کلیدی در تضمین صحت و کارایی حل مسائل PDE دارند. در این مطلب به معرفی و اهمیت این شرایط می‌پردازیم.

برای حل معادلات دیفرانسیل جزئی (PDE)، معمولاً باید علاوه‌بر خود معادله، شرایط تکمیلی مشخص شوند. مهم‌ترین آن‌ها عبارت‌اند از:

1. شرایط اولیه (Initial Conditions):
مربوط به زمانی مشخص شده هستند و وضعیت اولیه متغیر را مشخص می‌کنند (مثلاً توزیع دما یا سرعت اولیه).

2. شرایط مرزی (Boundary Conditions):
رفتار تابع روی مرز ناحیه مورد مطالعه را مشخص می‌کنند، از جمله:

• شرایط دیریکله (Dirichlet): مشخص کردن مقدار تابع روی مرز.
• شرایط نیومن (Neumann): مشخص کردن مشتق تابع روی مرز.
• شرایط رابین (Robin): ترکیبی از مقدار تابع و مشتق آن روی مرز.

3. شرایط سازگاری (Compatibility Conditions):
شرایطی هستند که باید هم‌زمان توسط شرایط اولیه و مرزی برآورده شوند تا مسأله دارای پاسخ یکتا باشد.

پس:
برای حل کامل یک PDE، علاوه‌بر فرم معادله، مشخص کردن شرایط اولیه، شرایط مرزی (دیریکله، نیومن، رابین) و همچنین رعایت شرایط سازگاری اهمیت اساسی دارند.

بعد این مقدمه بریم سراغ مطالب داخل جزوه:

شرایط در مشتقات جزئی

شرایط در کنار مسئله در مشتقات جزئی بسیار مهمه!

ما دو نوع شرط داریم: شرایط اولیه و شرایط مرزی

سه حالت داریم:

1) اگر در شرایطی که در مسئله وجود دارد، خود u باشد (شرایط دیریکله ای).

u(x,y,z,t) = g(x,y,z,t)

2) اگر مقدار مشتق تابع را در مرزها بدهند(شرایط نیومنی).

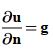
3) ترکیبی از حالت 1 و 2 باشد (هم خود u و هم مشتق u (شرایط رابینی)).

تار مرتعش

تاری داریم که در ابتدا و انتها ثابت کردهایم و میکشیم. میخواهیم بدانیم بعد از گذشت ، t نقطه x در چه موقعیتی قرار دارد (معادله موج) چند حالت وجود دارد:

1- جرم واحد طول تار ثابت است یعنی تار همگن و کشسان است و در مقابل خمش مقاومت ندارد.

2- نیروی گرانش قابل چشم پوشی است.

3- تار حرکات کوچکی در صفحه قائم دارد.

اگر 0 → Δx باشد، سمت چپ تعریف مشتق دوم u را نشان می دهد و داریم:

امیدوارم مطالب این جلسه براتون مفهوم بوده باشد. برای درک بیشتر حتما به مطالب جزوه در این لینک مراجعه کنید. برای دیدن محتوای ویدئویی آموزش هم به این آدرس در وبسایت ما مراجعه فرمایید.

از اینکه مثل همیشه با نوشتن نظرات ما را همراهی می کنید از شما سپاسگزارم.

موفق باشید.