آموزش تابع توزیعهای حاشیهای؛ آمار و احتمال مهندسی؛ جلسه 12
- آمار و احتمال
- نرگس دارابی
- 2 دقیقه
سلام و عرض ادب خدمت دوستان عزیزم امیدوارم حال دلتون عالی باشه ؛ در ادامه مباحث متغیرهای تصادفی امروز قصد داریم به میحث تابع توزیع حاشیه ای بپردازیم. همراهی شما تا انتها موجب دلگرمی ما خواهد بود.
توزیعهای حاشیه ای
تابع توزیع حاشیهای، یکی از مفاهیم پایهای در آمار و احتمال است که به ما امکان میدهد توزیع یک متغیر تصادفی را بهتنهایی بررسی کنیم، حتی زمانی که با چند متغیر دیگر بهصورت مشترک مدلسازی شده باشد. در واقع، این تابع با حذف اثر سایر متغیرها، نمایی سادهتر از رفتار یک متغیر خاص ارائه میدهد و نقش مهمی در تحلیل دادههای چندمتغیره و درک ساختار توزیع دارد.
 اگر توزیع احتمال توام یا تابع چگالی احتمال توام دو متغیر تصادفی معلوم باشد، آیا میتوان توزیع هر کدام را به صورت جداگانه معلوم کرد؟
اگر توزیع احتمال توام یا تابع چگالی احتمال توام دو متغیر تصادفی معلوم باشد، آیا میتوان توزیع هر کدام را به صورت جداگانه معلوم کرد؟
 بله میتوان. یعنی اگر Fx,y(x,y) معلوم باشد، میتوان Fx(x), fy(y) را بدست آورد.
بله میتوان. یعنی اگر Fx,y(x,y) معلوم باشد، میتوان Fx(x), fy(y) را بدست آورد.
بله میتوان یعنی اگر معلوم باشد میتوان به دست آورد.
و اما سوال بعدی:
 اگر توزیع های دو یا چند متغیر معلوم باشد و بدانیم وقوع آنها به طور همزمان میسر است، آیا می توان توزیع احتمال توام یا تابع چگالی احتمال توام آنها را به دست آورد؟
اگر توزیع های دو یا چند متغیر معلوم باشد و بدانیم وقوع آنها به طور همزمان میسر است، آیا می توان توزیع احتمال توام یا تابع چگالی احتمال توام آنها را به دست آورد؟
 خیر مگر اینکه متغیر تصادفی مستقل باشد.
خیر مگر اینکه متغیر تصادفی مستقل باشد.
اگر X,Y دو متغیر تصادفی با تابع احتمال توام (تابع چگالی احتمال توام) Fx,y(x,y) باشند، توزیع احتمال هر یک از متغیرهای تصادفی X,Y را به تنهایی با Fx(x), fy(y) نشان میدهیم و داریم:
در حالت پیوسته :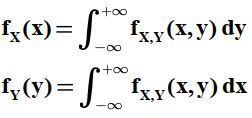
در حالت گسسته:
Fx(x), fy(y) را تمرین توزیع حاشیه ای مینامند.
مثال) با استفاده از جدول زیر فرض کنید X,Y دارای توزیع احتمال توام است. توزیع های حاشیه ای Fx(x), fy(y) را بنویسید. این مثال را با من همراه باشید تا با هم حل کنیم. مثال بعدی با شما.


چون مقادیر 2و 4 را اختیار می کند، پس داریم:



![]()

حال به صورت همزمان نشان می دهیم:

خب این هم حل مثال. برای دیدن توضیح این مثال به لینک ویدئویی موجود در وبسایت ما از این لینک می توانید مراجعه کنید. اگر هم صرفا دوست داید به مطالب این جلسه دسترسی داشته باشید، می توانید از این آدرس در کانال یوتیوب ما اقدام کنید. فراموش نکنید که بطور همزمان باید از جزوه هم استفاده کنید. این آدرس برای تهیه جزوه این فصل هست.
توی سه جلسه بعدی از جوه براتون کلی مثالهای متفاوت گنچاندم که با پیدا کرد پاسخ هر کدام، شما بیشت به مطالب اشراف پیدا خواهید کرد.
مطابق همیشه سپاسگزارم تا انتها همراه ما بودید.
موفق باشید










